프로그래머가 보는 수학 - 최대공약수와 최소공배수

사전지식 : https://aaaag.tistory.com/23

프로그래머가 보는 수학 - 소인수분해

---

최대공약수 : 공통의 약수중 최대 큰 약수

서로소 : 최대공약수의 값이 한 개밖에 없을 경우 서로소

---

126, 540의 최대공약수는

나눈수만 곱한다

2 * 3² == 18

최대 공약수는 18이고 18의 약수들을 126과 540의 공약수라 한다

126과 540의 공약수 == 18 공약수 1, 2, 3, 6, 9, 18

 

126, 540의 최대공약수는

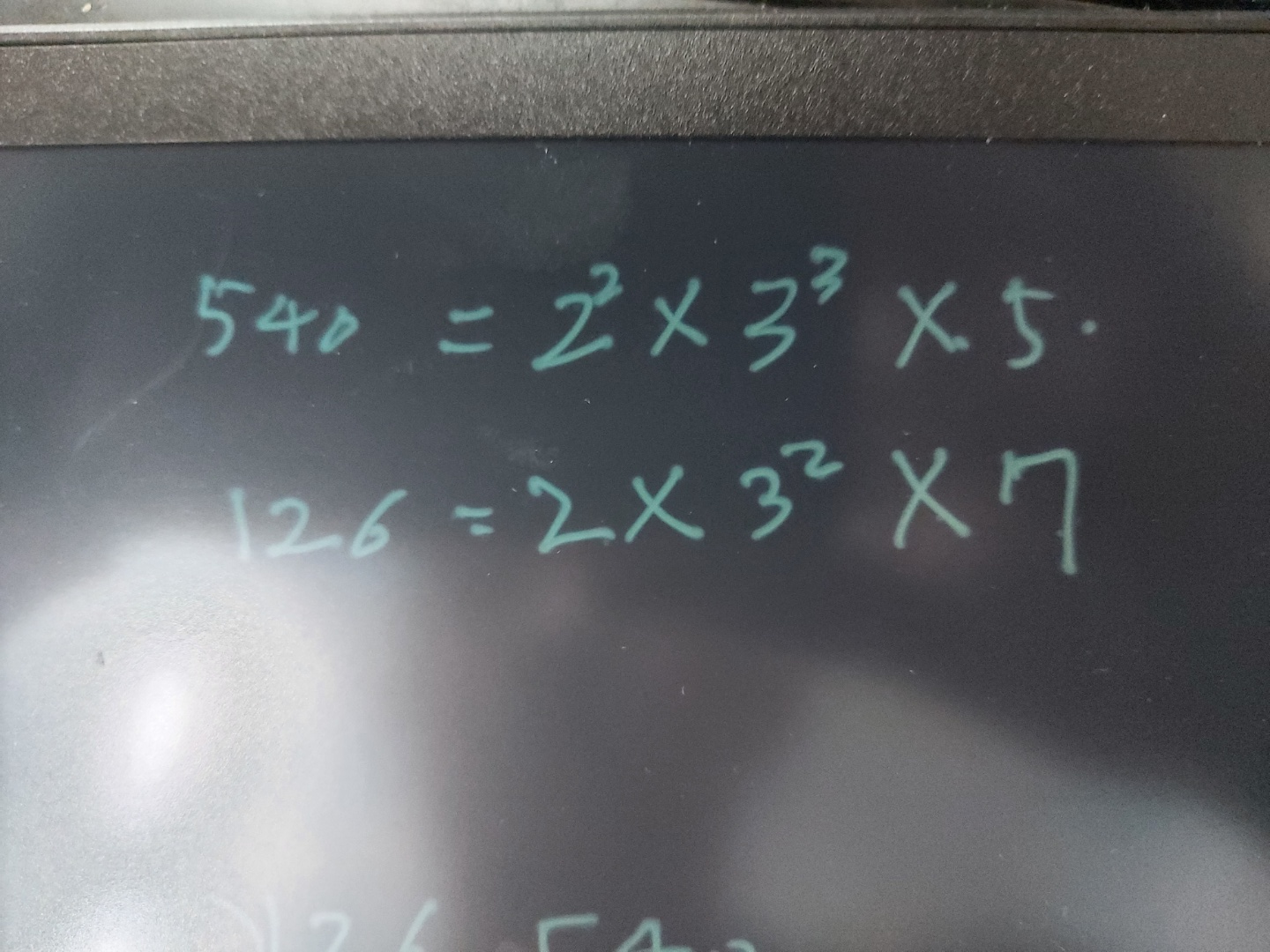
각각의 수를 소인수분해한다

공통된 밑 중 지수가 작은 것들을 곱하면 2 * 3² == 18

결과는 예1과 같다

 

5와 7의 최대공약수는 1

5와 7은 서로소이다.

---

프로그래밍 구현

# -*- coding: utf-8 -*-
import sys

firstNumber = int(input())
secondNumber = int(input())
#90 12

result = 1
divisor = 2
loopCheck = True
while loopCheck == True:
    firstResult = firstNumber % divisor
    secondResult = secondNumber % divisor
    if (firstResult == 0) and (secondResult == 0):
        firstNumber = firstNumber / divisor
        secondNumber = secondNumber / divisor
        result = result * divisor
        continue

    divisor = divisor + 1
    if (divisor > firstNumber) and (divisor > secondNumber):
        break

print(f"result : {result}")

---

최소공배수 : 공통의 배수중 최소 작은 배수

---

36, 150의 최소공배수는

공약수 3,2에 서로소 6,25도 가치 곱한다

2 * 3 * 6 * 25 == 900

최소공배수는 900이고 900의 배수들을(900, 1800, 2700...) 36과 150의 공배수라 한다

 

36, 150, 1080의 최소공배수는

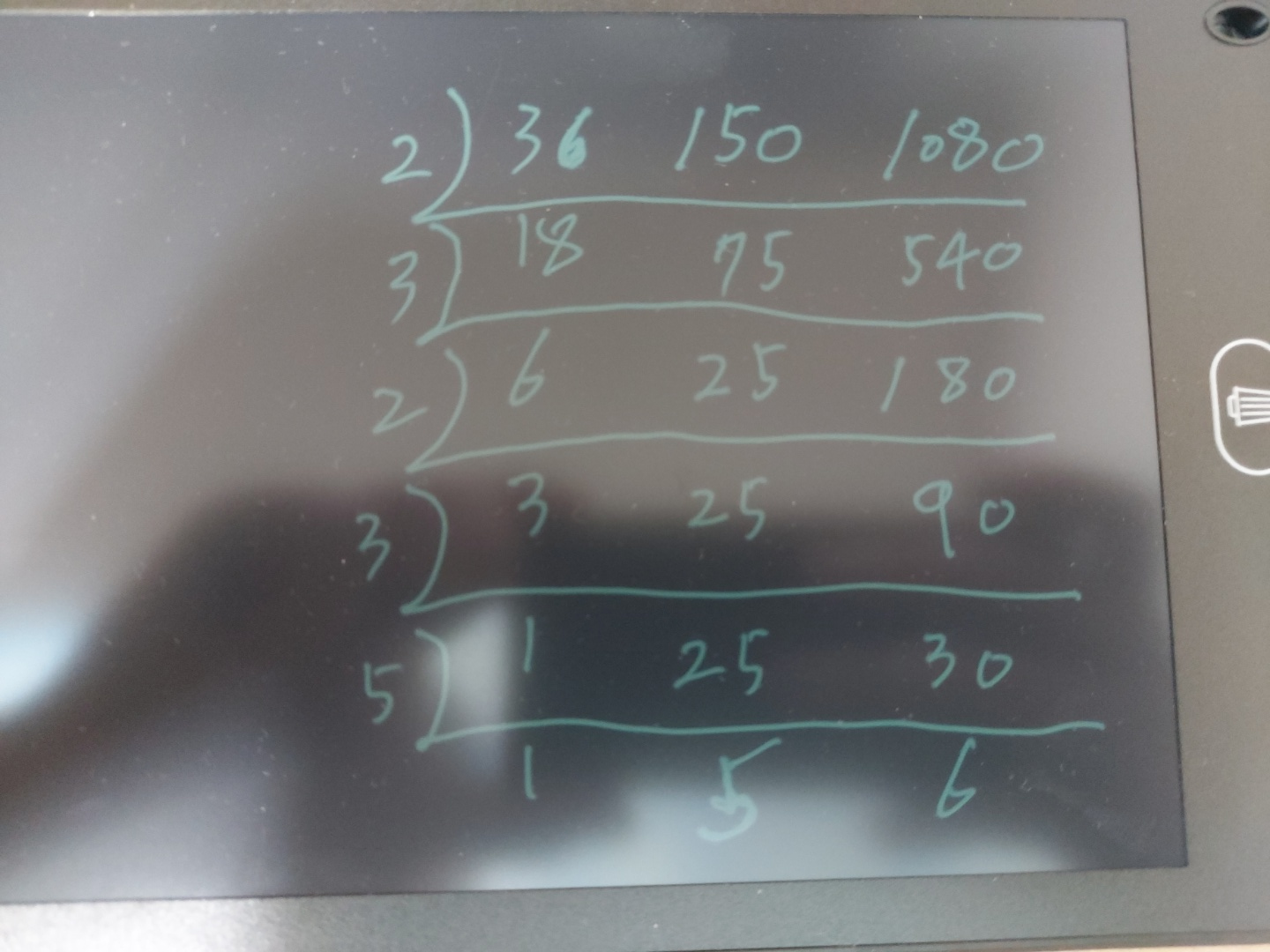
36, 150, 1080의 공약수가 아니더라도 나눈 다음 36, 150, 1080의 서로소가 나올 때 서로소 까지 곱한다

2³ * 3³ * 5² == 5,400

최소공배수는 5400

 

지수를 이용해서 최소공배수를 구할 때 36, 150, 1080을 각각 소인수 분해하면

36 == 2² * 3²

150 == 2 * 3 * 5²

1080 == 2³ * 3³ * 5

• 밑이 같지 않은 수도 포함해서 곱한다
• 밑이 같을경우 지수가 높은 것을 곱한다

2³ * 3³ * 5² == 5400

최소공배수는 5400

---

프로그래밍 구현

# -*- coding: utf-8 -*-
import sys

firstNumber = int(input())
secondNumber = int(input())
#36 150

result = 1
divisor = 2
loopCheck = True
while loopCheck == True:
    firstResult = firstNumber % divisor
    secondResult = secondNumber % divisor
    if (firstResult == 0) and (secondResult == 0):
        firstNumber = firstNumber / divisor
        secondNumber = secondNumber / divisor
        result = result * divisor
        continue

    divisor = divisor + 1
    if (divisor > firstNumber) and (divisor > secondNumber):
        result = result * firstNumber * secondNumber
        break

print(f"result : {int(result)}")

---

활용

• G는 최대 공약수
• L은 최소공배수
• A, B는 자연수
• x, y는 서로소
• L == G * x * y
• A = G * x
• B = G * y
• A * B == L * G

위 공식을 사용해서 예를 든다면

• 18, 50의 최대공약수(G)는 2
• 18, 50의 최소공배수(L)는 450
• 18(A) == 2(G) * 9(x)
• 50(B) == 2(G) * 25(y)
• 900(A * B) == 900(G * L)

---

프로그래밍 구현없음